Trie Data Structure

Tries are an extremely special and useful data-structure that are based on the prefix of a string. The prefix of a string is nothing but any n letters such that n ≤ |S| that can be considered beginning strictly from the starting of a string. The name trie comes from its use for retrieval.

A Trie is a special data structure used to store strings that can be visualized like a graph. It consists of nodes and edges. Each node consists of at max 26 children and edges connect each parent node to its children. These 26 pointers are nothing but pointers for each of the 26 letters of the English alphabet. A separate edge is maintained for every edge. Strings are stored in a top to bottom manner on the basis of their prefix in a trie. All prefixes of length 1 are stored at until level 1, all prefixes of length 2 are sorted at until level 2 and so on. Every node of Trie consists of multiple branches. Each branch represents a possible character of keys. We need to mark the last node of every key as end of word node.

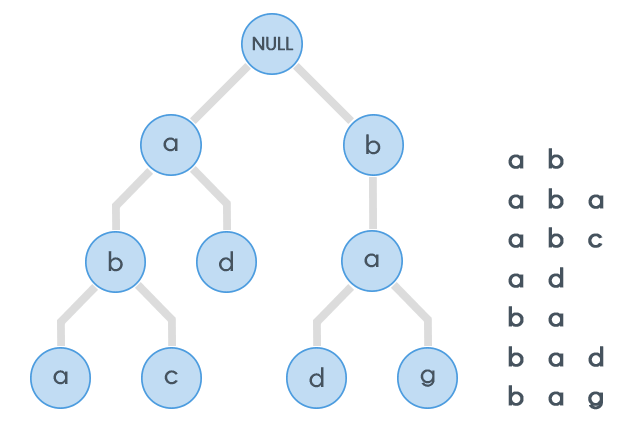
For example , consider the following diagram :

Trie Structure

A simple structure to represent nodes of English alphabet can be as following,

// Trie node
static class TrieNode
{
    TrieNode[] children = new TrieNode[ALPHABET_SIZE];
  
    // true if the node represents end of a word
    boolean isEndOfWord;
     
    TrieNode(){
        isEndOfWord = false;
        for (int i = 0; i < ALPHABET_SIZE; i++)
            children[i] = null;
    }
};

Inserting a key into Trie is simple approach. Every character of input key is inserted as an individual Trie node. Note that the children is an array of pointers (or references) to next level trie nodes. The key character acts as an index into the array children. If the input key is new or an extension of existing key, we need to construct non-existing nodes of the key, and mark end of word for last node. If the input key is prefix of existing key in Trie, we simply mark the last node of key as end of word. The key length determines Trie depth.

Searching for a key is similar to insert operation, however we only compare the characters and move down. The search can terminate due to end of string or lack of key in trie. In the former case, if the isEndofWord field of last node is true, then the key exists in trie. In the second case, the search terminates without examining all the characters of key, since the key is not present in trie.

During delete operation we delete the key in bottom up manner using recursion. The following are possible conditions when deleting key from trie,

1. Key may not be there in trie. Delete operation should not modify trie.
2. Key present as unique key (no part of key contains another key (prefix), nor the key itself is prefix of another key in trie). Delete all the nodes.
3. Key is prefix key of another long key in trie. Unmark the leaf node.
4. Key present in trie, having atleast one other key as prefix key. Delete nodes from end of key until first leaf node of longest prefix key.