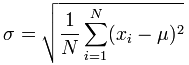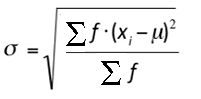Standard deviation is a measure of dispersement in statistics. “Dispersement” tells you how much your data is spread out. Specifically, it shows you how much your data is spread out around the mean.
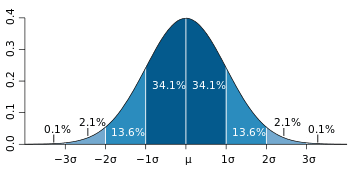
The bell curve (what statisticians call a “normal distribution“) is commonly seen in statistics as a tool to understand standard deviation. The following graph of a normal distribution represents a great deal of data in real life. The mean is represented by the Greek letter μ, in the center. Each segment (colored in dark blue to light blue) represents one standard deviation away from the mean. For example, 2σ means two standard deviations from the mean.
The bell curve above suggests that with reference to the mean (average) value –
- 68% of the data is clustered around mean within the 1st SD, in other words there is a 68% chance that the data lies within the 1st SD
- 95% of the data is clustered around mean within the 2nd SD, in other words there is a 95% chance that the data lies within the 2nd SD
- 99.7% of the data is clustered around mean within the 3rd SD, in other words there is a 99.7% chance that the data lies within the 3rd SD
Standard deviation tells how tightly data is clustered around the mean. When the bell curve is flattened (data is spread out), you have a large standard deviation — your data is further away from the mean. When the bell curve is very steep, your data has a small standard deviation — your data is tightly clustered around the mean. For example, the graph on the left might represent an abnormally high number of students getting scores close to the average, while the graph on the right represents more students getting scores away from the average.
This is the formula for Standard Deviation:
The Σ means “to add up”, so what you’re basically doing to find the sample standard deviation is adding your numbers, squaring them and dividing.
The formula to find the standard deviation for a frequency distribution is:
μ is the mean for the frequency distribution,
f is the individual frequency counts,
x is the value associated with the frequencies.