Introduction
Some applications involve grouping N distinct objects into a collection of Disjoint sets. Two important operations are then finding which set a given object belongs to and uniting the two sets.
A disjoint set data structure maintains a collection S={ S1 , S2 ,…, Sk } of disjoint dynamic sets. Each set is identified by a representative, which usually is a member in the set i.e. A disjoint-set (also called a union–find data structure or merge–find set) is a data structure that keeps track of a set of elements partitioned into a number of disjoint (non-overlapping) subsets.
Operations
The basic interface of this data structure consists of only three operations:
- make_set(v) – creates a new set consisting of the new element v
- union_set(a, b) – merges the two specified sets i.e. the set in which the element a is located, and the set in which the element b is located
- find_set(v) – returns the representative (also called leader) of the set that contains the element v. This representative is an element of its corresponding set. It is selected in each set by the data structure itself (and can change over time). This representative can be used to check if two elements are part of the same set or not. a and b are exactly in the same set, if find_set(a) == find_set(b). Otherwise they are in different sets.
Naive implementation of union_set() and find_set() has worst case liner time complexity. The trees created to represent subsets can be skewed and can become like a linked list. It can be optimized to O(Log n) in worst case.
Optimization
There are two techniques that significantly improve the performance of union-find data structures: union by rank and path compression.
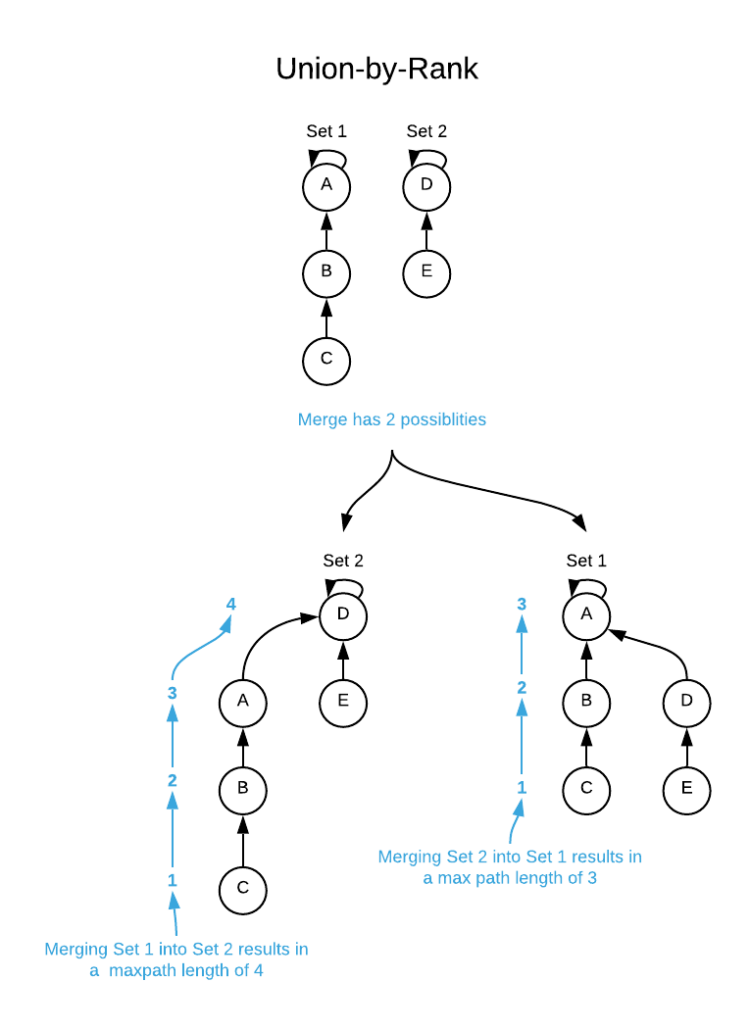
Union by rank ensures that when two sets are merged, each leaf of the tree will have the shortest possible path to the root. Shorter paths mean fewer traversals for each find operation. There are two possibilities for merging set-1 and set-2. If set-2 is consumed by set-1, it results in more work for the find operation. The idea is to always attach smaller depth tree under the root of the deeper tree. This technique is called union by rank.
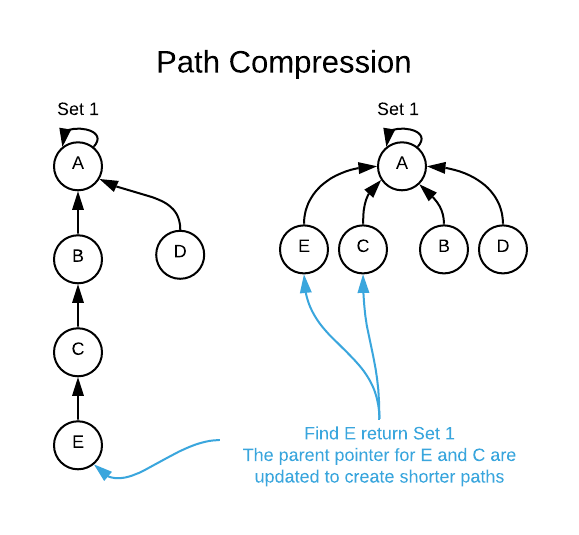
The second optimization to naive method is Path Compression. The idea is to flatten the tree when find_set() is called. When find_set() is called for an element x, root of the tree is returned. The find() operation traverses up from x to find root. The idea of path compression is to make the found root as parent of x so that we don’t have to traverse all intermediate nodes again. If x is root of a subtree, then path (to root) from all nodes under x also compresses. The two techniques complement each other.
Union-Find Algorithm can be used to check whether an undirected graph contains cycle or not. For each edge, make subsets using both the vertices of the edge. If both the vertices are in the same subset, a cycle is found.
Applications
Here we show two application examples.
- Connected components (CCs)
- Minimum Spanning Trees (MSTs)
