Backtracking

While solving a problem using recursion, we break the given problem into smaller ones. Let’s say we have a problem $A$ and we divided it into three smaller problems $B$, $C$ and $D$. Now it may be the case that the solution to $A$ does not depend on all the three subproblems, in fact we don’t even know on which one it depends.
Let’s take a situation. Suppose you are standing in front of three tunnels, one of which is having a bag of gold at its end, but you don’t know which one. So you’ll try all three. First go in tunnel $1$, if that is not the one, then come out of it, and go into tunnel $2$, and again if that is not the one, come out of it and go into tunnel $3$. So basically in backtracking we attempt solving a subproblem, and if we don’t reach the desired solution, then undo whatever we did for solving that subproblem, and try solving another subproblem.

Backtracking is a form of recursion. The usual scenario is that you are faced with a number of options, and you must choose one of these. After you make your choice you will get a new set of options; just what set of options you get depends on what choice you made. This procedure is repeated over and over until you reach a final state. If you made a good sequence of choices, your final state is a goal state; if you didn’t, it isn’t.

You want to get to a good leaf. At each node, beginning with the root, you choose one of its children to move to, and you keep this up until you get to a leaf. Suppose you get to a bad leaf. You can backtrack to continue the search for a good leaf by revoking your most recent choice, and trying out the next option in that set of options. If you run out of options, revoke the choice that got you here, and try another choice at that node. If you end up at the root with no options left, there are no good leaves to be found.

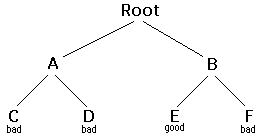
For the above tree

• Starting at Root, your options are A and B. You choose A.
• At A, your options are C and D. You choose C.
• C is bad. Go back to A.
• At A, you have already tried C, and it failed. Try D.
• D is bad. Go back to A.
• At A, you have no options left to try. Go back to Root.
• At Root, you have already tried A. Try B.
• At B, your options are E and F. Try E.
• E is good. Congratulations!