Asymptotic analysis of an algorithm refers to defining the mathematical boundation/framing of its run-time performance. When it comes to analysing the complexity of any algorithm in terms of time and space, we can never provide an exact number to define the time required and the space required by the algorithm, instead we express it using Asymptotic Notations.
The word Asymptotic means approaching a value or curve arbitrarily closely (i.e., as some sort of limit is taken). Following are the commonly used asymptotic notations to calculate the running time complexity of an algorithm.
- Ο Notation
- Ω Notation
- θ Notation
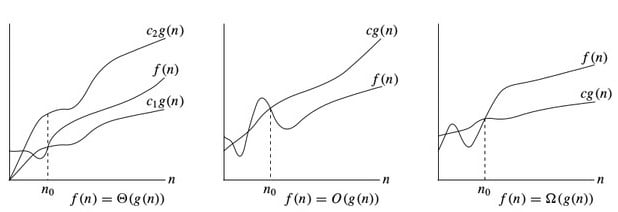
Theta Notation, θ
The notation θ(n) is the formal way to express both the lower bound and the upper bound of an algorithm’s running time.
For example, if for some algorithm the time complexity is represented by the expression 3n2 + 5n, then the time complexity would be Θ(n2), ignoring the constant coefficient and removing the insignificant part (5n). Complexity of Θ(n2) means, that the avaerage time for any input n will remain in between, k1 * n2 and k2 * n2, where k1, k2 are two constants, thereby tightly binding the expression representing the growth of the algorithm.
Big Oh Notation, Ο
The notation Ο(n) is the formal way to express the upper bound of an algorithm’s running time. It measures the worst case time complexity or the longest amount of time an algorithm can possibly take to complete.
Consider Linear Search algorithm, in which we traverse an array elements, one by one to search a given number. In Worst case, starting from the front of the array, we find the element or number we are searching for at the end, which will lead to a time complexity of n, where n represents the number of total elements. But it can happen, that the element that we are searching for is the first element of the array, in which case the time complexity will be 1. So worst case time complexity in big-O notation is O(n), which means that the time complexity will never exceed n, defining the upper bound, hence saying that it can be less than or equal to n.
Omega Notation, Ω
The notation Ω(n) is the formal way to express the lower bound of an algorithm’s running time. It measures the best case time complexity or the best amount of time an algorithm can possibly take to complete. This always indicates the minimum time required for any algorithm for all input values, therefore the best case of any algorithm. In simple words, when we represent a time complexity for any algorithm in the form of big-Ω, we mean that the algorithm will take atleast this much time to complete it’s execution. It can definitely take more time than this too.